Ok, for a change of pace let’s break away from sorting algorithms and do this problem:
Printing a Multiplication Table of the First 10 Prime Numbers
I got this as a coding challenge a few days ago and finally got a chance to tackle it this weekend. The prompt asks for the user to create a program that runs on the command line, and it should print out a multiplication table to STDOUT. I feel like I’ve seen similar problems elsewhere, but this one had the twist that it wanted the multiplier numbers to be primes.
Other rules: Make it flexible for N # primes, write some tests, don’t use Ruby’s Prime class, package yer code.
I started out this challenge by trying to understand clearly what the problem was. Print out a multiplication table? Like this?
Oooooooooooooh. Haven’t seen one of those in a long time.
So the top row and the first column would be populated with primes. Hmm…
Since I couldn’t use Ruby’s Prime class from the standard library, writing a method for finding primes seemed like the first thing to do.
I wanted to make my program flexible so you could create multiplication tables of different sizes. So I created a method to pull the first n primes into an array.
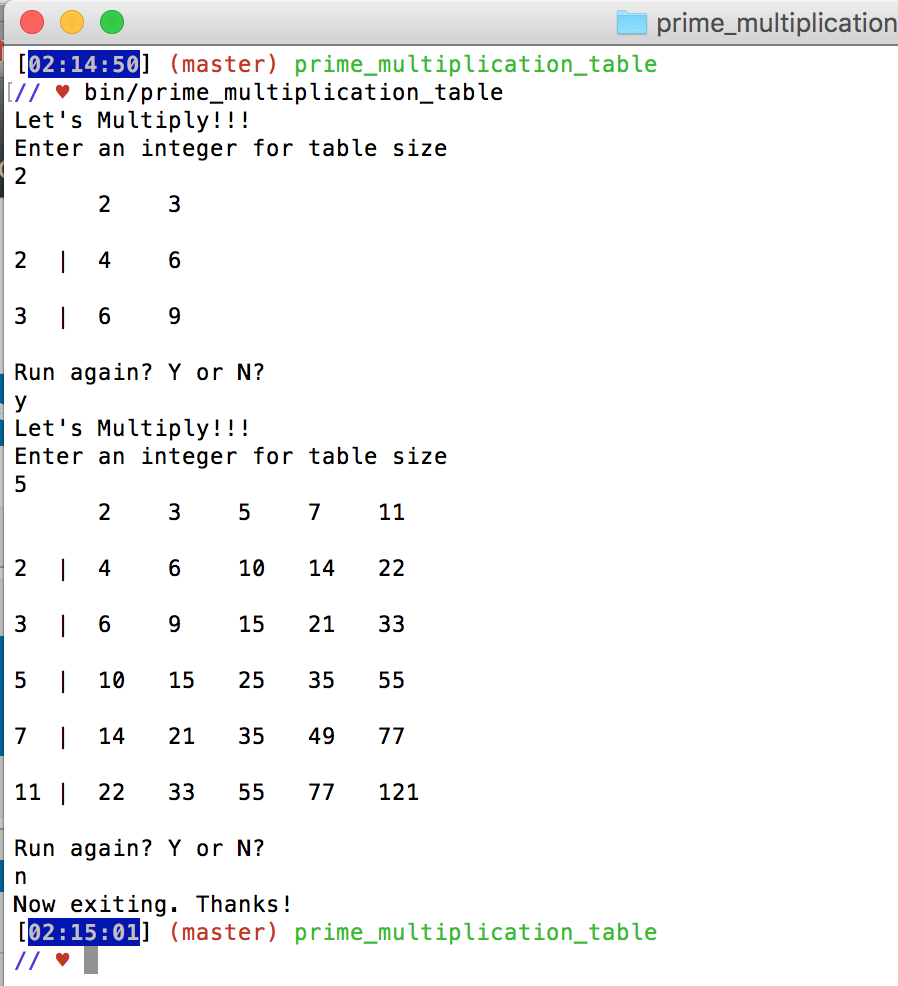
And finally actually printing out the actual table! Formatting was the biggest pain here.
After I was done with these methods, I thought I was good to go. HA! Nope, still got to package it up and write some tests. I was going back and forth, but I’ll talk about the tests first.
I decided to go with RSpec, so I created a gemfile and added in the requirement. Then I created some spec docs and started going to town. I really only had 3 methods to test, and I decided to do 2 tests for each. It’s been a while since I watched ThoughtBot’s TDD lecture, and my subscription to their site has lapsed, so I decided to keep it as simple as possible. An RSpec tutorial I was reading was referencing a “Calculator” class in its tests, so I thought “Oh, I might as well bundle up the 3 methods into a MultiplicationTable class.” So I went back and changed that, and my tests.
All of the tests were pretty simple except for the print_tables one. Again, it all came down to formatting. I wasn’t sure how to check what was being printed to STDOUT. I came across stringio and some helper methods on StackOverflow, threw them into my spec_helper, and then it was on. I could capture and check what was being printed to the console. Still, it was tricky to figure out what string I was looking for here. RSpec failure messages came to the rescue as I just copied the extremely ugly failure string (making sure #’s were correct) and pasted into my tests.
Hooray! My tests were looking for the right things now. Nevermind that when I ran the tests I got this little deprecation warning:
Um… ok. Sure I can go back and change that easily. Nope, getting errors after I tried to fix it. I’ll go back and deal with it later.
I started out thinking about how to package my program. My mind wandered to gems, which of course made me think about my NPR Stories Gem. I looked at my gem to check out the basic structure, see what I was still missing in my multiplication table project. Then I got sidetracked for about 30 minutes trying to push my NPR gem to RubyGems. I hadn’t yet actually published my NPR gem for a variety of different failures, but this time I realized one major reason- I had to actually build the gem first with:
gem build npr_stories.gemspec
then I could push it to RubyGems. D’oh. That was embarrassing. Now that it was published, and robots were already scraping it, I wanted to make sure that it worked, so I spent some more time trying to edit and test my NPR gem, then I remembered that I had to finish this coding challenge. Right. And of course there was a typo in my gemspec file. Not worth doing a whole gem update for a single letter typo.
Ok, back to multiplication tables! So I could package this multiplication table as a gem for easy installation…But is it even worth it? If so, I should have set this up as a gem to begin with so I could have used this bundler command that pulls together all those files and folder structure for you:
$ bundle gem my_gemI decided to do it anyways and created a new repo to play with. I just copied over my tiny amount of code thus far.
15 minutes later I abandoned ship and returned to my original repo. Creating a gem just didn’t make sense to me for something so small. Hmmmm… how did I want this to run on the command line? I created a bin folder & executable, and also a CLI class with a simple interface.
And after a few hiccups it’s working!
The last step I had was to write a README doc. Whew! That was a lot of work for such a simple little ask. It would have gone faster if I hadn’t indulged my little diversions to other projects and down multiple rabbit holes.